| sen |  |  |  |  | 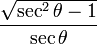 |  |
|---|---|---|---|---|---|---|
| cos |  | 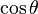 | 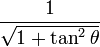 |  | 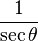 | 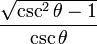 |
| tan | 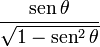 |  |  | 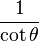 |  |  |
| cot |  |  | 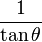 |  |  |  |
| sec |  |  | 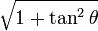 |  |  |  |
| csc |  |  | 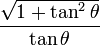 |  |  | 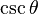 |
De las definiciones de las funciones trigonométricas:











Son más sencillas de probar en la circunferencia trigonométrica o goniométrica (que tiene radio igual a 1):
A veces es importante saber que cualquier combinación lineal de una serie de ondas senoidales que tienen el mismo pero están desfasadas, es también una onda senoidal del mismo período pero con un desplazamiento de fase diferente. Dicho de otro modo:
Es llamada identidad trigonométrica fundamental, y efectuando sencillas operaciones permite encontrar unas 24 identidades más, muy útiles para problemas introductorios del tipo conocido el valor de la función seno, obtenga el valor de las restantes (sin tabla ni calculadora).
Por ejemplo, si se divide ambos miembros por cos², se tiene:
Calculando la recíproca de la expresión anterior:
Entonces puede expresarse la función seno según alguna otra conocida:
y análogamente con las restantes funciones .
Teoremas de la suma y diferencia de ángulos
Pueden demostrarse según la Fórmula de Euler o mediante la proyección de ángulos consecutivos. La identidad de la tangente surge del cociente entre coseno y seno, y las restantes de la recíproca correspondiente.
Para ángulos opuestos:
Identidades del ángulo múltiple
Identidades del ángulo doble, triple y medio
Pueden obtenerse remplazándolo y por x (o sea  ) en las identidades anteriores, y usando el teorema de Pitágoras para los dos últimos (a veces es útil expresar la identidad en términos de seno, o de coseno solamente), o bien aplicando la Fórmula de De Moivre cuando n = 2.
) en las identidades anteriores, y usando el teorema de Pitágoras para los dos últimos (a veces es útil expresar la identidad en términos de seno, o de coseno solamente), o bien aplicando la Fórmula de De Moivre cuando n = 2.
 ) en las identidades anteriores, y usando el teorema de Pitágoras para los dos últimos (a veces es útil expresar la identidad en términos de seno, o de coseno solamente), o bien aplicando la Fórmula de De Moivre cuando n = 2.
) en las identidades anteriores, y usando el teorema de Pitágoras para los dos últimos (a veces es útil expresar la identidad en términos de seno, o de coseno solamente), o bien aplicando la Fórmula de De Moivre cuando n = 2.| Fórmula del ángulo doble | |||
|---|---|---|---|
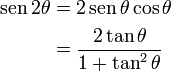 |  |  | 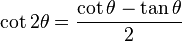 |
| Fórmula del ángulo triple | |||
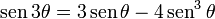 | 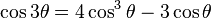 |  | |
| Fórmula del ángulo medio | |||
 | 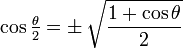 |  | 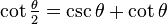 |
Producto infinito de Euler
Identidades para la reducción de exponentes
Resuelve las identidades tercera y cuarta del ángulo doble para cos²(x) y sin²(x).
| Seno | 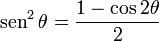 |  | |
|---|---|---|---|
| Coseno | 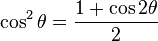 |  | 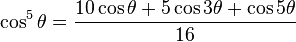 |
| Otros |  | 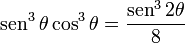 |
Paso de producto a suma
Puede probarse usando el teorema de la suma para expandir los segundos miembros.
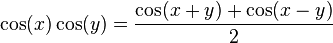

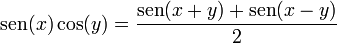
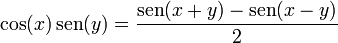
- Deducción de la identidad
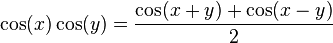
Sabemos por el teorema de la suma y la resta que:
Si separamos la suma de la resta quedan entonces los dos posibles casos:
1): 
2):

2):

Si tomamos la ecuación 1) y despejamos cos(x)cos(y) nos queda que:
3): 

Y si sumamos el miembro de la derecha de la ecuación 2) al miembro izquierdo de la ecuación 3), y para mantener la igualdad se suma el lado izquierdo de la ecuación 2) en el lado derecho de la ecuación 3). (Recuerda que si se suma un elemento a ambos lados de la ecuación se mantiene la misma), quedaría:
Simplificando el elemento sin(x)sin(y) y sumando cos(x)cos(y) quedaría:
- 2cos(x)cos(y) = cos(x + y) + cos(x − y)
Y por último multiplicando ambos lados de la ecuación por ½ queda:
Nota 1: este procedimiento también se puede aplicar para demostrar el origen de las otras dos ecuaciones simplemente cambiando los valores.
Nota 2: Usando 3) y el resultado anterior se obtiene también:
Notar el cambio de signo.
Paso de suma a producto
Reemplazando x por (a + b) / 2 e "y por (a – b) / 2 en las identidades de producto a suma, se tiene:
Paso de diferencia de cuadrados a producto


Deducción
1) recordando:que cateto opuesto sobre cateto adyacente


multiplicando

Sabemos que:


el la primera ecuación transponemos  y en la segunda
y en la segunda 
 y en la segunda
y en la segunda 
De tal manera que obtendremos:


aplicando esto en la ecuación inicial

multiplicando

De una manera análoga se halla el segundo teorema.
Eliminar seno y coseno
A veces es necesario transformar funciones de seno y coseno para poderlas sumar libremente, en estos casos es posible eliminar senos y cosenos en tangentes.
Funciones trigonométricas inversas
Composición de funciones trigonométricas
|
|
|
Fórmula de productos infinitos
| Seno | Coseno |
|---|---|
|
|
|
Fórmula de Euler
Historia
Los Elementos de Euclides, que datan del siglo III a. C., contienen ya una aproximación geométrica de la generalización del teorema de Pitágoras: las proposiciones 12 y 13 del libro II, tratan separadamente el caso de un triángulo obtusángulo y el de un triángulo acutángulo. La formulación de la época es arcaica ya que la ausencia de funciones trigonométricas y del álgebra obligó a razonar en términos de diferencias de áreas. Por eso, la proposición 12 utiliza estos términos:
«En los triángulos obtusángulos, el cuadrado del lado opuesto al ángulo obtuso es mayor que los cuadrados de los lados que comprenden el ángulo obtuso en dos veces el rectángulo comprendido por un lado de los del ángulo obtuso sobre el que cae la perpendicular y la recta exterior cortada por la perpendicular, hasta el ángulo obtuso.»

Euclides, Elementos.
Siendo ABC el triángulo, cuyo ángulo obtuso está en C, y BH la altura respecto del vértice B (cf. Fig. 2 contigua), la notación moderna permite formular el enunciado así:
Faltaba esperar la trigonometría árabe-musulmana de la Edad Media para ver al teorema evolucionar a su forma y en su alcance: el astrónomo y matemático al-Battani generalizó el resultado de Euclides en la geometría esférica a principios del siglo X, lo que permitió efectuar los cálculos de la distancia angular entre el Sol y la Tierra. Fue durante el mismo período cuando se establecieron las primeras tablas trigonométricas, para las funciones seno y coseno. Eso permitió a Ghiyath al-Kashi matemático de la escuela de Samarcanda, de poner el teorema bajo una forma utilizable para la triangulación durante el siglo XV. La propiedad fue popularizada en occidente por François Viète quien, al parecer, lo redescubrió independientemente.
Fue a finales del siglo XVII cuando la notación algebraica moderna, aunada a la notación moderna de las funciones trigonométricas introducida por Euler en su libro Introductio in analysin infinitorum, permitieron escribir el teorema bajo su forma actual, extendiéndose el nombre de teorema (o ley) del coseno.
Teorema del seno
En todo triángulo se da la siguiente relación entre la longitud de sus lados a, b y c y el seno de sus respectivos ángulos opuestos A, B y C

Demostración
Dado el triángulo ABC, denotamos por A su circuncentro y dibujamos su circunferencia circunscrita. Prolongando el segmento BO hasta cortar la circunferencia, se obtiene un diámetro BP.
Ahora, el triángulo PBC es recto, puesto que BP es un diámetro, y además los ángulos A y P son iguales, porque ambos son ángulos inscritos que abren el segmento BC (Véase definición de arco capaz). Por definición de la función trigonométrica seno, se tiene






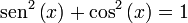

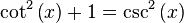


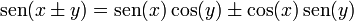
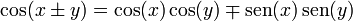

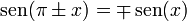

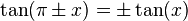
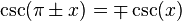
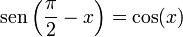
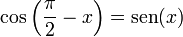

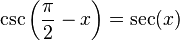










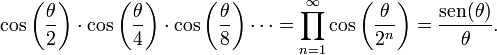











![\tan[\arcsin (x)]=\frac{x}{\sqrt{1 - x^2}}](http://upload.wikimedia.org/wikipedia/es/math/b/3/8/b38e763c095868afbdd990ac46f684e9.png)
![\tan[\arccos (x)]=\frac{\sqrt{1 - x^2}}{x}](http://upload.wikimedia.org/wikipedia/es/math/3/5/f/35f8c64aca700f0fc661b01653a72ca2.png)
![\cos[\arctan(x)]=\frac{1}{\sqrt{1+x^2}}](http://upload.wikimedia.org/wikipedia/es/math/e/3/a/e3a7c52ccbf1c1ec0bce78efbb522f39.png)
![\cos[\arcsin(x)]=\sqrt{1-x^2} \,](http://upload.wikimedia.org/wikipedia/es/math/0/2/b/02bd50b439936a0b929aa5a6b523622e.png)















No hay comentarios:
Publicar un comentario