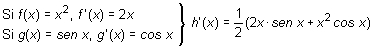Derivada de una función constante
Sea una función constante f(x) = C.
Su gráfica es, como se sabe, una recta paralela al eje de abscisas. Puesto que para cualquier valor de la abscisa su ordenada correspondiente es, constantemente, igual a C, si a es un punto cualquiera del campo de definición de f(x),
f(a + h) - f(a) = C - C = 0, por lo que
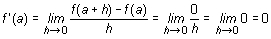
Luego la derivada de una constante es siempre cero.
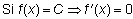
Derivada de la función lineal mx + b
Sea una función lineal cualquiera f(x) = mx + b. Para un punto cualquiera x,
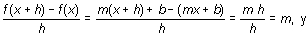
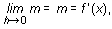 lo cual significa que la derivada de una recta coincide con la pendiente de ella misma y, en consecuencia, la tangente en un punto a una recta es la propia recta.
lo cual significa que la derivada de una recta coincide con la pendiente de ella misma y, en consecuencia, la tangente en un punto a una recta es la propia recta.
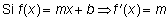
Derivada de una constante por una función, k · f(x)
Si k es una constante y f(x) una función, la derivada de la nueva función k · f(x) será:
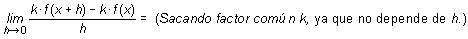
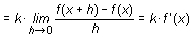
Se ha demostrado que (k · f(x))' = k · f'(x) Así, para derivar una expresión de la forma
k · f(x), basta derivar la función f(x) y multiplicar después por la constante k.
Derivada de la función potencia xm (m un número natural)
Para calcular la derivada de la función f(x) = xm, m > 0, hay que evaluar el cociente
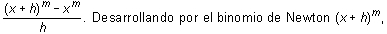
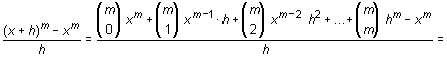
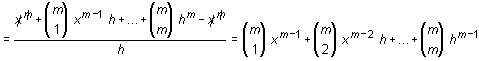
Tomando límites cuando h --> 0,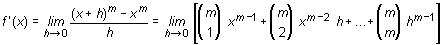
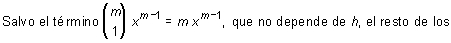
sumandos tiende a cero (su límite es cero).
Se concluye que
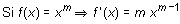
Ejercicio: cálculo de derivadas
Calcular la derivada de f(x) = x2 en el punto de abscisa - 1.Resolución:
f '(x) = 2 · x2 - 1 = 2 x
f '(- 1) = 2 · (- 1) = - 2
Entonces, la pendiente de la tangente a la parábola y = x2 en x = - 1 es - 2.
Derivadas de las funciones trigonométricas sen x y cos x
La derivada de la función f(x) = sen x es f '(x) = cos x
La derivada de la función g(x) = cos x es g '(x) = - sen x
Si necesitas las demostraciones dímelo.
Derivada de la función logaritmo neperiano ln |x|
Puesto que el logaritmo está definido sólo para valores positivos y distintos de cero, es necesario considerar el logaritmo del valor absoluto de x.Para calcular la derivada de esta función se han de considerar dos casos, x > 0 y x < 0:
a) Si x es positivo, aun tomando h negativo, x + h es positivo si se toman valores de h suficientemente pequeños, lo cual es posible pues se va a calcular el límite cuando h tiende a cero. En estas condiciones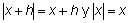
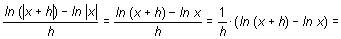
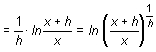 Por tanto, si x > 0
Por tanto, si x > 0
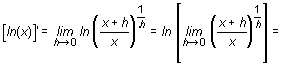
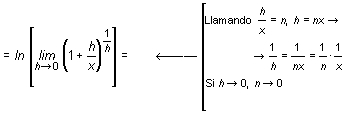
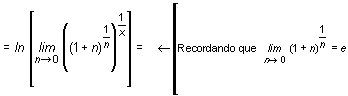
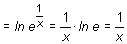
b) Si x es negativo, aun tomando h positivo y suficientemente pequeño, x + h sigue siendo negativo y |x + h| = - (x + h) y |x| = - x.

Como se aprecia, se llega a la misma expresión que en el caso anterior y la demostración se continuaría de forma idéntica.
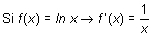
Derivadas de las funciónes exponenciales ax y ex
Sea la función y = ax, siendo a una constante positiva distinta de 1. La derivada de esta función en un punto x es:
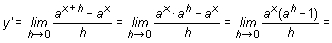
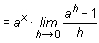
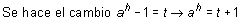
y se toman logaritmos neperianos:
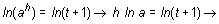
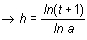
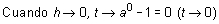
Luego:
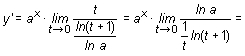
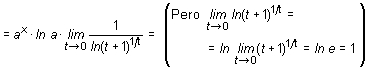
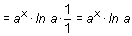
En particular, cuando la constante a es el número e, la derivada de la función ex es
(ex )' = ex · ln e = ex · 1 = ex
Hasta el momento se saben derivar algunas funciones elementales pero no hay nada que permita encontrar las derivadas de una suma, un producto o un cociente de estas derivadas; se requiere, por consiguiente, seguir avanzando en la obtención de propiedades encaminadas a este fin.
Operaciones con funciones
Hay que recordar cómo se definen la suma, el producto y el cociente de funciones. Si f y g son dos funciones definidas en un mismo intervalo (en caso contrario, alguna de estas operaciones podría no estar definida),
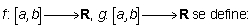
Función suma de f y g como la nueva función f + g: [a,b] ---> R,
(f + g) (x) = f(x) + g(x)
Función producto de f y g como la función f ·g: [a,b] ---> R,
(f · g) (x) = f(x) · g(x)
siempre que g(x) distinto de 0 para todo x del intervalo.
Derivada de una suma de funciones
Si f y g son dos funciones derivables en un mismo punto x de un intervalo, la derivada de la función suma en dicho punto se obtiene calculando
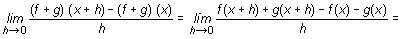
La derivada de una suma es igual a la suma de las derivadas.
[f(x) + g(x)] ' = f '(x) + g '(x)
Derivada de una diferencia de funciones
f - g = f + (- g), por lo que [f(x) + (- g(x))]' = f'(x) + (- g(x))'
Pero - g(x) = (- 1) · g(x) y la derivada de una constante por una función es igual al producto de la constante por la derivada de la función:
[- g(x)]' = [(- 1) · g(x)]' = (- 1) · g'(x) = - g'(x)
En consecuencia,
[f(x) - g(x)]' = f'(x) - g'(x)
Ejercicio: cálculo de derivadas
Calcular la derivada de la función f(x) = x - cos xResolución:

Calcular la derivada de f(x) = x3 - sen x + ln|x| en el punto x = -p/3.
Derivada de un producto de funciones
Sean f y g dos funciones definidas y derivables en un mismo punto x.
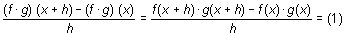
Si se suma y se resta en el numerador f(x) · g(x + h), la fracción anterior no varía,
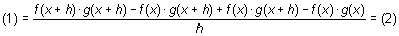 Sacando g(x + h) factor común en los dos primeros sumandos, y f(x) en los otros dos,
Sacando g(x + h) factor común en los dos primeros sumandos, y f(x) en los otros dos, 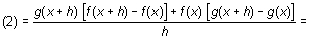

Si ahora se toman límites cuando h tiende a cero,
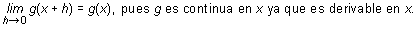
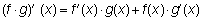
Ejercicio: cálculo de derivadas
Hallar la derivada de h(x) = x · ln x para cualquier x positivo.
Resolución:
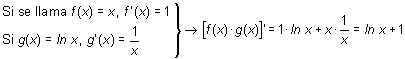
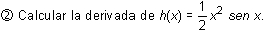
Resolución: